Absolute Magnitude and Distance Modulus
Absolute Magnitude and Distance Modulus
The apparent brightness of a star depends upon their intrinsic brightness or luminosities (The total amount of radiant energy emitted per second from the surface of stars) and also on their distance from the observer. Since the distance vary continuously the apparent magnitudes(m) do not provide the actual brightness or luminosities. To get actual brightness or luminosities of stars the term Absolute magnitude was introduced.
Absolute Magnitude(M) of a star is defined as the apparent magnitude of the star if the star was placed at a standard distance of 10 par sec. The absolute magnitude of a star depends on the actual or intrinsic brightness and not on the distance from the observer.
[extra info]
Relation between Apparent Magnitude(m) and Absolute Magnitude(M)
Let Bm be the brightness of a star with magnitude m and is at a distance d, BM be the brightness of another star with magnitude M and is at a distance D
The Brightness of a star is inversely proportional to the square of the distance
Since M is the absolute magnitude and D is the
standard distance 10 parsec, logD = log10 = 1
This is the fundamental relation between the Apparent magnitude(m) and the Absolute Magnitude(M). The quantity m-M depends only on the distance d and is called Distance Modulus.
The absolute magnitude of normal stars lies between -10 and 20.





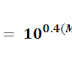






No comments: